BIENVENIDOS !!
En el día de hoy, intentaremos explicar las medidas de tendencia central, posición y dispersión.
Es importante saber antes de empezar, que dichas medidas solo son aplicables a variables cuantitativas.
Dentro de las cuales existen dos tipos distintos: Continuas y discretas, que fueron explicadas detalladamente en la entrada del tema anterior (Tema 7).
Existen tres grandes tipos de medidas estadísticas:
- Medidas de Tendencia central: nos indican en torno a qué valor (centro) se distribuyen los datos.
- Medidas de posición: dividen un conjunto de datos en grupos con el mismo número de individuos. Para calcular las medidas de posición es necesario que los datos estén ordenados de menor a mayor.
- Medidas de dispersión o variabilidad: da información acerca de la heterogeneidad de nuestras observaciones.
MEDIDAS DE TENDENCIA CENTRAL.
Encontramos:
Media aritmética o media (x): Es la suma de todos los valores de la variable observada entre el total de observaciones.
Por ejemplo: Si queremos calcular la nota media de una clases de 10 sujetos, donde las notas son: 5, 7, 8, 9, 10, 4, 4, 8, 5 y 4'5.
Sumamos todas las notas de clases y la dividimos entre el número de notas, es decir:
5+7+8+9+10+4+4+8+5+4.5 / 10;
64'5 / 10 = 6'45;
Por lo que 6'45 sería la media de clase.
Mediana: representa el valor de la variable de posición central en un conjunto de datos ordenados.
- Si el número de observaciones es impar: el valor de la observación será justamente la observación que ocupa la posición central.
Por ejemplo: Si tenemos 5 datos, que ordenados son: 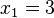 ,
, 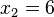 ,
, 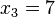 ,
, 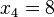 ,
, 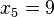 => El valor central es el tercero:
=> El valor central es el tercero: 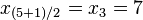 . Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (
. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo ( ,
,  ) y otros dos por encima de él (
) y otros dos por encima de él ( ,
,  ).
).
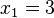 ,
, 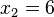 ,
, 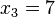 ,
, 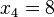 ,
, 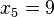 => El valor central es el tercero:
=> El valor central es el tercero: 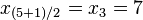 . Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (
. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo ( ,
,  ) y otros dos por encima de él (
) y otros dos por encima de él ( ,
,  ).
).- Si el número de observaciones es par: el valor de la mediana corresponde a la media entre los dos valores centrales, es decir, la media entre la observación n/2 y la observación (n/2)+1.
Por ejemplo: Tenemos cuatros sujetos de edades: 10, 15, 20 y 25. Cogemos a los dos sujetos centrales y hacemos la media aritmética de ambos.
15+20 / 2 = 17'5.
Moda: Es el valor con mayor frecuencia, es decir, que más veces se repite. Se puede dar que existan dos modas, en este caso se llama bimodal, o más de dos modas, en este caso se llama multimodal.
Es IMPORTANTE saber, que se puede aplicar para variables cuantitativas y variables cualitativas.
MEDIDAS DE POSICIÓN.
Encontramos:
Cuantiles: Se calculan para variables cuantitativas y, al igual que la mediana, sólo tienen en cuenta la posición de los valores de la muestra.
Los cuantiles más usados son:
- Percentiles: Divide la muestra ordenada en 100 partes. Es importante saber que el p50 corresponde al valor de la mediana.
- Deciles: Dividen la muestra ordenada en 10 partes.
- Cuartil: Dividen la muestra ordenada en 4 partes.
El primer cuartil Q1 = Indica el valor que ocupa una posición en la serie numérica de forma que el 25% de las observaciones son menores y que el 75% son mayores.
El segundo cuartil Q2 = indica el valor que ocupa una posición en la serie numérica de forma que el 50% de las observaciones son menores y que el 50% son mayores.
El tercer cuartil Q3 = indica el valor que ocupa una posición en la serie numérica de forma que el 75% de los observaciones son menores y que el 25% son mayores.
El cuarto cuartil Q4 = indica el valor mayor que se alcanza en la serie numérica.
-Para entenderlo vamos a poner un ejercicio explicativos.
Tenemos la siguiente tabla:
-Calcularemos: cuartiles, percentiles y deciles.
CUARTILES.
Número total = n; donde n=40
Para calcular Q1 = n x 25 / 100 = 10.
Una vez que hemos calculado Q1 = 10, nos fijamos en la frecuencia absoluta (Fi), y vemos donde esta el valor 10.
Donde Fi es igual a 10, en relación con Xi es igual a 4'2. Eso quiere decir que el 25% de niños pesan menos de 4'2 Kg, y el 75% restante pesa más de 4'2 Kg.
Para calcular Q2 = n x 50 / 100 = 40 x 50 / 100 = 20.
Nos fijamos en la tabla donde Fi = 20, y nos fijamos en el valor de Xi, donde es igual a 4'5.
Esto quiere decir que el 50% de los niños pesas menos de 4'5 Kg, y el 50% restante pesa más de 4'5 Kg.
El mismo procedimiento se realizará para Q3 y Q4
PERCENTILES
Supongamos que queremos calcular el percentil 30, es decir P30 (30%).
Se realiza de la siguiente manera: P30 = n x 30 / 100 = 12.
Observamos en la columna de Fi, el 12, como no hay el número exacto cogeremos el siguiente número que le sigue es decir el número Fi = 14, que se corresponde con el Xi= 4'3.
Eso significa que el 30% pesa menos de 4'3 Kg y el 70% restante pesa más de 4'3 Kg.
DECILES
Supongamos que queremos calcular el decil 1, es decir D1.
Se realiza de la siguiente manera: D1= n x 1 / 10 = 4.
Al igual que en los anteriores cálculos nos fijamos en la Fi.
En este caso cuando Fi = 6, Xi = 3'9. Eso quiere decir que el 1 de cada 10 niños pesa menos de 3'9Kg y 9 de cada 10 pesa más de 3'9Kg.
MEDIDAS DE DISPERSIÓN
La información que nos aporta las medidas de tendencia central son limitadas. A través de las medidas que se va a explicar a continuación, nos proporciona mayor información.
En este vídeo, se explica claramente:
- Rango o recorrido.
- Desviación media.
- Varianza.
- Desviación estándar.
En el siguiente vídeo adjunto se explicará: el coeficiente de variación:
DISTRIBUCIONES NORMALES.
En
estadística se llama distribución normal, distribución de Gauss o distribución
gaussiana, a una de las distribuciones de probabilidad de variable continua que
con más frecuencia aparece en fenómenos reales. Es Distribución de probabilidad
más frecuente con variables continuas, por ejemplo, altura, peso, niveles de
colesterol…
Las
distribuciones normales en un histograma aparece una especie de Campana, por
eso la campana de Gauss. Y es simétrica respecto de los valores de posición
central, es decir que la moda va a coincidir con la media y la mediana.
|
Media, moda, mediana.
|
La gráfica de su
función de densidad tiene una forma acampanada y es simétrica respecto de los
valores posición central (media, mediana y moda, que coinciden en estas
distribuciones). Es simétrica dejando la mitad de los valores
por debajo del punto máximo y la mitad de los valores por encima.
Una
distribución normal sigue estos principios básicos: si al valor de la media le
restamos y le sumamos una desviación típica, si la serie numérica siguiera una
distribución normal (como el colesterol). Dice que el 68.25% de las
observaciones se va a sumar entre los valores de la suma y la resta de la media
a una desviación típica. Estas datos varían si sumamos una, dos o tres
desviaciones típicas.
ASIMETRÍA Y CURTOSIS
La asimetría
es al lado contrario al que vemos el pico (la moda), es decir si vemos el pico
hacia la derecha la asimetría es a la izquierda, y si la moda está a la
izquierda la asimetría esta hacia la derecha.
Coeficiente de asimetría de una variable:
Grado de asimetría de la distribución
de sus datos en torno a su media, cuanto más asimétrica sea, valores más
diferentes encontraremos. Es adimensional.
Asimetrías:
Los
resultados pueden ser los siguientes:
-
g1=0
(distribución simétrica; existe la misma concentración de valores a la derecha
y a la izquierda de la media).
-
g1>0
(distribución asimétrica positiva; existe mayor concentración de valores a la derecha de la media que a su izquierda).
-
g1<0
(distribución asimétrica negativa; existe mayor concentración de valores a la
izquierda de la media que a su derecha).
CURTOSIS O APUNTAMIENTO DE LA CURVA.
No tiene
relación con la simetría. Coeficiente de apuntamiento o curtosis de una
variable, sirve para medir el grado de concentración de los valores que toma en
torno a su media. Los datos se acumulan mucho, mientras más se acumulen, más
apuntada esta la curva.
Se elige
como referencia una variable con distribución normal, de modo que para ella el
coeficiente de curtosis es 0.
Los
resultados pueden ser los siguientes:
-
g2=0
(distribución mesocúrtica o normal). Presenta un grado de concentración medio
alrededor de los valores centrales de la variable (el mismo que presenta una
distribución normal). Presentan un grado de concentración medio a los valores de la media.
-
g2>0
(distribución leptocúrtica). Presenta un elevado grado de concentración
alrededor de los valores centrales de la variable.
-
g2<0
(distribución platicúrtica). Presenta un reducido grado de concentración
alrededor de los valores centrales de la variable.









No hay comentarios:
Publicar un comentario